本科目を履修する上での注意事項

授業の目的と内容

本授業では、自然科学や工学の事象の正確な表現に必須となる数学的方法のうち，「線形代数学」の内容を一通り身につけることを目標とする．

1次独立性・ベクトル空間等の基礎概念を理解した上で線形写像・固有値・行列の対角化について学ぶ。

達成目標

  1. ベクトル、行列の基本的な計算ができる。（30%）
  2. 基底、線形写像について理解し、具体的問題に応用できる。（45%）
  3. 固有値、固有ベクトルを計算でき、具体的問題に応用できる。（25%）

また, 本科目はJプログラムにおける学習・教育達成目標「C:科学と技術の基礎知識を習得している。(科学技術の知識)」の「(2) 機械工学に必要な自然科学の基礎を習得している。」に対応している.

授業の予定と記録

第1回 4月 12日（木） ガイダンス，ベクトルの演算と内積  1 §1   1 §2  / 配布プリント
【キーワード】幾何ベクトル, 位置ベクトル, 数ベクトル, ベクトルの線形演算, ベクトルの大きさ, 内積, 単位ベクトル, 逆ベクトル
第2回 19日（木） ベクトル空間  5 §16  / 配布プリント
【キーワード】$n$次元数ベクトル, 内積, シュワルツの不等式, ベクトルのなす角, （２つのベクトルの）直交条件・平行条件, 基本ベクトル
第3回 26日（木） 正規直交系  5 §18 
【キーワード】正規直交系, グラムシュッミットの方法, クロネッカーの $\delta$ 記号
問題：p.112 問2
第4回 5月 10日（木） ベクトル空間の部分空間  5 §19.1 
【キーワード】部分空間, 線形条件, 線形結合
問題：p.115 問2
第5回 17日（木） 部分空間の基底と次元  5 §17   5 §19.2   5 §20 
【キーワード】1次独立, 1次従属, 基底
問題：（与えられたベクトルの組が）1次独立か1次従属か判定しなさい.
第6回 24日（木） 部分空間の積・和  5 §21 (〜p.124) 
【キーワード】次元, 積空間, 和空間, 直和
問題：p.128 問2（$W_1$ と $W_2$ の和と積を求めなさい）
31日（木） （休講）
第7回 6月 7日（木） 部分空間の直交補空間  5 §21.5   5 §21.6 , 線形写像  6 §23 (〜p.138 例4) 
【キーワード】直交補空間, 直和分解, 線形写像, 線形変換（1次変換）, 表現行列
問題：p.144 問1 線形変換 $f$ の表現行列を求めなさい.
第8回 14日（木） 線形写像の合成  6 §23.5 , 正則変換  6 §24 
【キーワード】合成写像, 上への１対１写像, 逆写像, 正則変換
問題：p.140 問4 (i) $f$, $g$, および $g\circ f$ がどこからどこへの写像か答えなさい. (ii) $g\circ f$ の表現行列を求めなさい. (iii) $f\circ g$ が定義可能か考察しなさい.
p.144 問1 線形変換 $f$ が正則変換か否か判定し, 正則ならば, 逆変換 $f^{-1}$ の表現行列を求めなさい.
第9回 21日（木） 直交変換  6 §25 
【キーワード】直交行列, 直交変換, 正規直交系（再）, 転置行列
問題：行列 $S_\theta=\left(\begin{array}{rr}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)$ と $T_\theta=\left(\begin{array}{rr}\cos\theta&\sin\theta\\\sin\theta&-\cos\theta\end{array}\right)$ に対して, (i) これらが直交行列であることを示しなさい. (ii) $\theta=0$, $\pi$, $\pi/2$ のとき, $T_\theta$ が定める1次変換がどのような変換か考察しなさい.
p.153 問6
第10回 28日（木） 固有値・固有ベクトルの定義と求め方  7 §27.1   7 §27.2   7 §27.3 
【キーワード】固有値, 固有ベクトル, 固有多項式, 固有方程式
問題：p.167 問1 (1)〜(8)（固有値が実数のもののみ考える. また, 固有空間は求めなくてよい）
第11回 7月 5日（木） 固有ベクトルと固有空間  7 §27.2   7 §28.5   7 §31.2   7 §31.3 
【キーワード】固有空間, 固有空間分解, 対称行列
問題：(i) p.167 問1 (1)〜(8) の固有空間を求めなさい（ただし, 固有値が実数のもののみ考える）
(ii) 問1 (7)〜(12) の中で, 対称行列をすべて選びなさい.
第12回 12日（木） 行列の対角化  7 §30.5   7 §30.6 
【キーワード】対角行列, 対角成分, 対角化, 対角化可能性
問題：p.184 問5 (1)〜(8) の各行列 $A$ について対角化可能か否か判定し, 対角化できる場合は, $P^{-1}AP$ が対角行列となるような正則行列 $P$ を求め, $P^{-1}AP$ がどのような対角行列になるか答えなさい（ただし, $A$ の固有値が実数のもののみ考える）.
第13回 19日（木） 対称行列の対角化  7 §31 
【キーワード】対称行列（再）, 直交行列（再）, 正規直交系（再）
問題：p.192 問3 (1)〜(4)
第14回 23日（月） 2次形式の標準化  8 §32 （スライド ）【補講日：2時限, 1-256教室】
【キーワード】2次形式, 2次曲線, 2変数関数の極値
問題：p.201 問2 (1)〜(6) の2次形式の標準形を求めなさい.
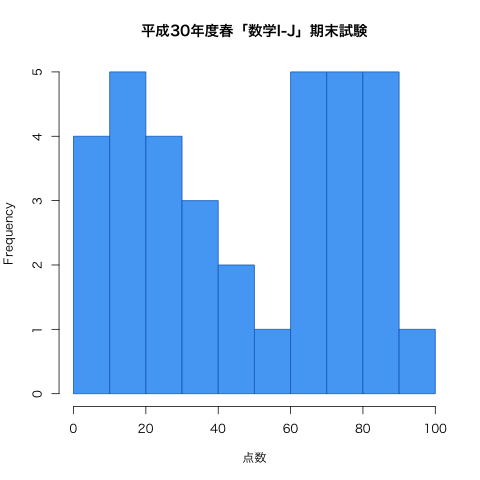
26日（木） 期末試験（問題 | 解答 | 得点分布）

教科書・参考文献について

評価について

履修登録前の準備

試験の得点分布と評価など