連絡事項

  • 連絡事項については 日本工大サポータル の掲示板をメインに使っていきます. 定期的に確認するようにしてください.
  • Twitter (@shiroyasu_NIT) でも, 授業に関する情報を発信していきます（ハッシュタグは #18Fam2J ）. 質問, 意見などのリプライを歓迎します.
  • 授業に対する基本的な考え方にも目を通しておいてください.
  • 9/2：このページを公開しました.

    • 授業の目的

    本授業では、自然科学や工学の事象の正確な表現に必須となる数学的方法のうち、「微分方程式論」の内容を一通り身につけることを目的とする。

    変数分離形、同次形といった代表的な微分方程式の解法を学び、線形微分方程式について学ぶ。

    達成目標

    1. 変数分離形、同次形の微分方程式が解ける。（20%）
    2. 積分因子を含めた完全微分方程式が解ける。（20%）
    3. 線形微分方程式の理論に慣れ、解法を熟知する。（60%）

    また, 本科目はJプログラムにおける学習・教育達成目標「C:科学と技術の基礎知識を習得している。(科学技術の知識)」の「(2) 機械工学に必要な自然科学の基礎を習得している。」に対応している.

    授業の予定と記録

    第1回 9月 27日（木） ガイダンス
    微分方程式とその解，一般解・特殊解・特異解  第1部 第1章 §1, 2 
    第2回 10月 4日（木） 変数分離形  第1部 第2章 §1 
    問題：p.11 問題1 (1)(2)
    第3回 11日（木） 同次形  第1部 第2章 §2 
    問題：p.13 問題1 (1)(2), 問題2
    第4回 18日（木） 1階線形微分方程式  第1部 第2章 §3 p.14--15 
    問題：p.15 問1, p.16 問題3 (1)(2)
    第5回 25日（木） ベルヌーイの方程式  第1部 第2章 §3 p.15--16 （【休講】を取りやめました）
    問題：p.16 問題2 (1)(2)(3), 3 (3)
    第6回 11月 1日（木） 完全微分方程式  第1部 第2章 §4 
    問題：p.22 問題1 (1)(2)(3)
    第7回 8日（木） 積分因子  第1部 第2章 §4 
    問題：p.22 問題2, 3
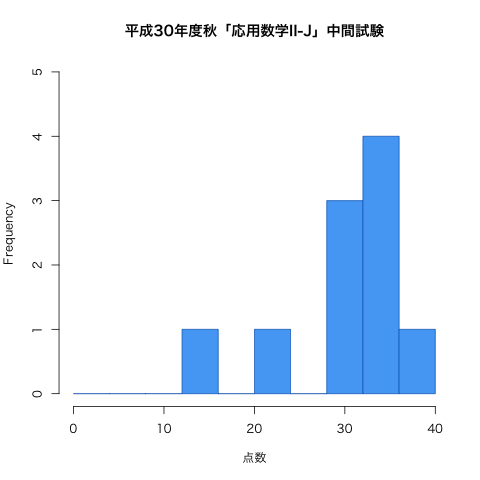
    第8回 15日（木） 中間試験（問題 | 解答 | 得点分布）
    第9回 22日（木） 線形微分方程式の解の性質  第1部 第3章 §1 
    第10回 29日（木） 微分演算子  第1部 第3章 §2 
    問題1：(i) $(D^2-D-2)e^{2x}$ と $(D^2-D-2)x^2$ を計算しなさい.
    (ii) (i)の結果から, $y=e^{2x}$ は2階定数係数線形微分方程式[　　]の解であり, $y=x^2$ は2階定数係数線形微分方程式[　　]の解であることがわかる. [　　]に入る微分方程式を答えなさい.
    問題2：$f(t)=t-2$ に対して, 次を計算しなさい; (i) $f(D)e^{3x}$ (ii) $f(D)(e^{3x}x^2)$ (iii) $f(D+3)x^2$
    第11回 12月 6日（木） 定数係数線形同次微分方程式の一般解  第1部 第3章 §3 
    問題：p.43 問題1
    第12回 13日（木） 定数係数線形微分方程式の解の性質  第1部 第3章 §5 p.52 
    逆演算子①  第1部 第3章 §4 (〜p.47, 公式(1)〜(5)） 
    問題：p.47 問題1
    第13回 20日（木） 逆演算子②  第1部 第3章 §4 (p.47〜49 公式(6),(7)） 
    未定係数法①  第1部 第3章 §5（p.56 定理3.8） 
    問題：p.49 問題2(1)
    第14回 1月 10日（木） 逆演算子③  第1部 第3章 §4 (p.49,50 公式(8)） 
    未定係数法②  第1部 第3章 §5（p.54 定理3.6, p.55 定理3.7） 
    問題：p.53 問1, p.55 問2(2), p.55 問3, p.57 問4(3)
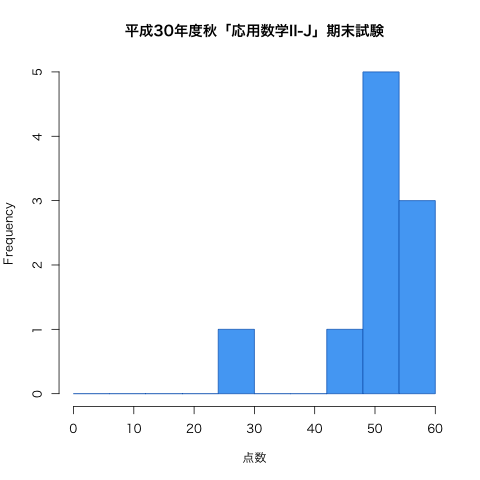
    24日（木） 期末試験（問題 | 解答 | 得点分布）

    教科書・参考文献について

    評価について

    履修登録前の準備

    試験の得点分布と評価など