home ›› Teaching ›› NIT ››
2014年度春学期 微分積分学 II Differential and Integral Calculus II
火2限 10:55-12:35 | 2-273教室 | 対象:ものづくり環境学科2年生 創造システム工学科2年生
担当:佐藤 弘康(hiroyasu [at] nit.ac.jp | W1棟204 | 0480-33-7972)
連絡事項
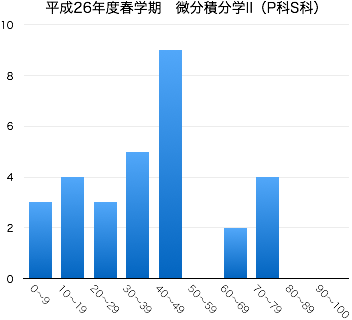
- 8/18:期末試験の解答および,得点分布(このページの最下部を参照)などを公開しました.
- 7/29:本日は期末試験でした.これをもってこの授業はすべて終了しました.
- 7/2:6月10日に説明する予定だった「無理関数の不定積分」の音声つきスライド動画をYouTubeに公開しました.7月15日までの都合のいい時間に受講(閲覧)してください.
- 6/19:小テストの解答を公開しました.[3] の問題はミスがあります.$I$の被積分関数「$x^x\,\cos 3x$」は「$e^x\,\cos 3x$」の間違いです(試験時に訂正しました).
- 6/17:6月10日に実施できなかった小テストを「6月17日(火)」と「6月18日(水)」の6時限に実施します.都合のいい日に受験してください.試験会場
については決まり次第速やかに掲示しますはいずれの日も2-274教室です. - 5/30:6月10日に小テストを実施します(授業時間内,30分程度).6月3日までに扱った内容(「原始関数」「不定積分の計算」)が試験範囲です.授業中の問題演習で解いてもらった問題,または例題として解説した問題の中から出題します(これまでのノート,答案を確認してください).
- 4/7:このページを公開しました.
- Twitterでこの授業についてツイートしていきます(ハッシュタグは#14S微積2PS.ツイログはこちら).質問,意見などのリプライを歓迎します.
- 授業に対する>基本的な考え方にも目を通しておいてください.
授業の目的
自然科学のみならず工学のさまざまな分野で、現象を表現・解析する手段として微分積分学の知識は欠かせない。 微分積分学の概念・計算技法を身につけるために、1変数関数を対象とした積分法について学習する。基礎的な計算技法に習熟するとともに、図形の面積・体積や曲線の長さへの応用について理解する。
達成目標
- 初等関数の原始関数を求めることができる。
- 置換積分法を利用して原始関数を求めることができる。
- 部分積分法を利用して原始関数を求めることができる。
- 初等関数の定積分を求めることができる。
- 広義積分を求めることができる。
- 積分の計算技法を用いて、図形の面積・体積、曲線の長さを求めることができる。
科目の位置づけ
- 微分積分学I(1変数関数の微分) → 微分積分学II(1変数関数の積分) → 微分積分学III(多変数関数の微積分)
授業の予定と記録
| 第1回 | 4月 | 8日(火) | ガイダンス,1変数関数の微分法の復習 |
| 第2回 | 15日(火) | 不定積分の基本概念 第1章 §2.1 | |
| 第3回 | 22日(火) | 初等関数の原始関数 (1) 整式 第4章 §1.1 (p.113-116) | |
| 第4回 | 30日(水) | 初等関数の原始関数 (2) 指数関数・三角関数 第4章 §1.1 (p.116,117) 置換積分法 (1) 第4章 §2.1(p.121) |
|
| 第5回 | 5月 | 13日(火) | 置換積分法 (2) 第4章 §2.1(p.122,123) 第4章 §1.2 |
| 第6回 | 20日(火) | 部分積分法 第4章 §2.2 | |
| 第7回 | 27日(火) | 三角関数の不定積分 第4章 §3.1, 3.2 | |
| 第8回 | 6月 | 3日(火) | 部分分数分解,有理関数の不定積分 第4章 §4.1 第4章 §1.2 |
| 第9回 | 10日(火) | 急用により休講 web 補講「無理関数の不定積分」動画 スライド 第4章 §4.2 第4章 §1.2 | |
| 第10回 | 17日(火) | 定積分の定義とその基本性質,微分積分学の基本定理 第1章 §2.2 第5章 §1.1, 1.2, 1.3 定積分の計算 (1) 初等関数 第5章 §2.1 |
|
| (補講) | (6時限)小テスト(中間試験) 問題 解答 | ||
| (補講) | 18日(水) | (6時限)小テスト(中間試験) 問題 解答 | |
| 第11回 | 24日(火) | 定積分の計算 (2) 置換積分法・部分積分法 第5章 §2.2, 2.3 | |
| 第12回 | 7月 | 1日(火) | 定積分の計算 (3) 偶関数と奇関数 |
| 第13回 | 8日(火) | 広義積分 第5章 §3.1, 3.2 | |
| 第14回 | 15日(火) | 面積 第5章 §4.1 | |
| 29日(火) | 期末試験 (10:40 -- 11:40, 1-255教室) 問題 解答 |
教科書・参考文献について
- 矢野健太郎・石原繁編 『微分積分』 裳華房 » リンク
評価について
- 期末試験80点,小テスト・演習課題など20点の配点で評価する.
- 中間期にミニ中間試験を実施する(10点).
- 毎回の授業で問題演習を実施する(手順は以下).
- 教科書等の問題を指定し,指定の答案用紙に解答.
- 一定時間の後,各自答え合わせ(必要に応じて解説).
- 授業終了時に答案用紙を回収.
期末試験の得点分布と評価など
 |
|